Level 5: A short solution is as follows: Label the edges going around in a clockwise direction (starting anywhere) as E1, E2, E3, E4, E5, E6. The following sequence of flips solves the level: E1, E3, E5, E2, E4, E6, E1, E3, E5.
Level 6: This level is the same as the previous one in that the starting and ending configurations stand in the same relation to each other. The same solution works here.
Levels 5, 6, 7: The basic move consists in alternatively doing flips on two sides of a triangle (a total of four flips). Say: E1, E2, E1, E2. This has the effect of leaving all triangles unchanged except the one with sides E1 and E2, which ends up being rotated. Equipped with this move and some trial and error these levels can be solved from any shuffled position. The following analysis shows how to remove the trial and error.
A triangle can be in any of these six positions:

Starting with the top left triangle, the triangles on the first row can be obtained by a rotation, while to get to the triangles in the bottom row we need a reflection (a flip) along one of the axes of symmetry of the triangle.
To solve Levels 5,6,7 from any shuffled configuration, we keep track of which triangles in the initial configuration are in a “reflected” state relative to the final configuration. In order for the puzzle to be solvable, the number of triangles in a reflected state must be even. To solve the puzzle, we identify which triangles are in a reflected state. With a few carefully chosen flips we “unreflect” them all (they must each be flipped once). Then we apply the basic move described above to rotate each triangle to its final position.
All the configurations of the figure from Levels 5,6,7 can be put into either the configuration from Level 5 or the one from Level 6. On the other hand, these two configurations cannot be connected by a sequence of flips (the number of reflected triangles is odd).
Levels 9, 10, 11, 12: The same basic move (alternatively flipping on two sides) can be applied to any polygon. It rotates it by a certain angle while leaving the rest of the polygons unchanged. Again, this and some trial and error solves all these levels.
Here is how to do things more systematically. Hexagons behave the same as triangles. They can be in either a reflected or rotated state with respect to each other. There is one small complication in identifying reflected hexagons. Consider the following two hexagons:
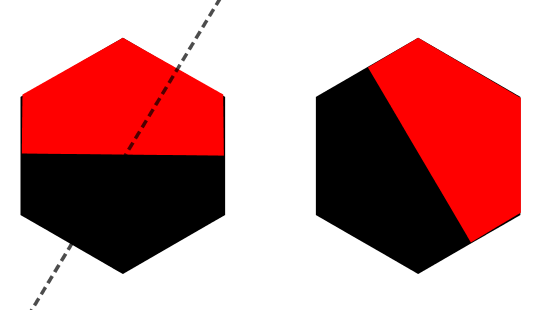
Even though it is possible to rotate one into the other by a 60 degrees rotation, these rotations never arise while playing the game (since we only reflect hexagons along axes going through their sides, never through a vertex). In fact, in the game these two hexagons are in reflected state with respect to each other. If the decoration of the hexagons was richer, it would be apparent that it is a reflection that takes one into the other (along the axis indicated by a dotted line).
Level 9: We can draw a diagram where each node represents one of the polygons of the figure and where each node has a 0 or a 1 depending on whether the polygon is reflected or not relative to its final state. The lines connecting nodes in the diagram indicate which polygons are simultaneously affected by a flip. Here is the diagram for Level 9:
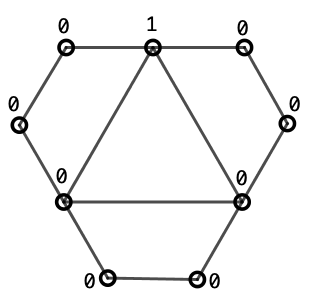
A flip here means adding 1 modulo 2 to all the nodes along a line. It is easy to turn this diagram into “all zeros” after a few steps. Back in the game, these operations leave all triangles and hexagons in a rotated state. We can then rotate one by one using the basic move.
The same strategy applies to Levels 10, 11, 12 starting from any shuffled configuration.
Similar considerations apply to figures composed of polygons whose number of sides is not a multiple of 4. If the number of sides is a multiple 4 (squares, octagons,…), things are a little different, but in a way that makes the puzzle easier.
Levels 13: After reaching the right configuration for the squares, the green node ends up in a corner.. There is a simple technique for “passing around” the green node, bringing it back to the center.
Levels 13-18: Solve the level ignoring the green nodes. Then pass them around to their desired positions.
Level 19: Go around clockwise tapping at the edges: E1, E2, E3, E4, E1, E2… The level is solved after 12 flips.
Levels 20-22: These levels can be solved using the same general strategy: solve for the polygons first, then bring the nodes to their respective places. The latter may involve quite a bit of maneuvering (e.g., temporarily tucking a node in an inconspicuous place).
Level 23: There are a few moves that leave the nodes unchanged while flipping some of the polygons. This also works: Starting on the right hexagon edge and going clockwise for long enough solves the puzzle.